阪大の入試ミスとオーディオ

阪大の入試問題のミスが世間を賑わせていますが、そのミスの内容についてはあまり詳しく報道されることはありません。
もっぱら話題になるのは受験生が可哀想で、その社会的責任をどうするんだという話ばかりです。もちろん、本来は合格していたはずなのに不合格とされた受験生は気の毒といわざるを得ないのですが、人が生きるというのはそう言う「理不尽」に次々と出くわすと言うことです。
そんな「理不尽」にへこんでいたのでは前に進めないのですから、「既往は咎めず」という大きな心を持って、今の自分にとってどのように対処するのかがベターなのかという観点で賢く対処して欲しいものです。

不幸にあって嘆いている人に世間は同情は寄せますが、いつまでもへたり込んで泣いている人には冷たいものですから。

ですから、ここで取り上げたいのは、そう言う社会的な問題ではなくて、純粋にミスとなってしまった問題の中味についてです。
テレビ報道などではちらりと問題文が映るだけで、その内容については「どうせ説明しても分からないだろう！」と言うことで殆どふれていません。

ただ、音叉が出てきて、その周波数と壁からの距離が問題になっていると言うことで、あれっ、それってオーディオ絡みの問題じゃないの？と言うことで興味がひかれたわけです。
問題はこうなっているようです。

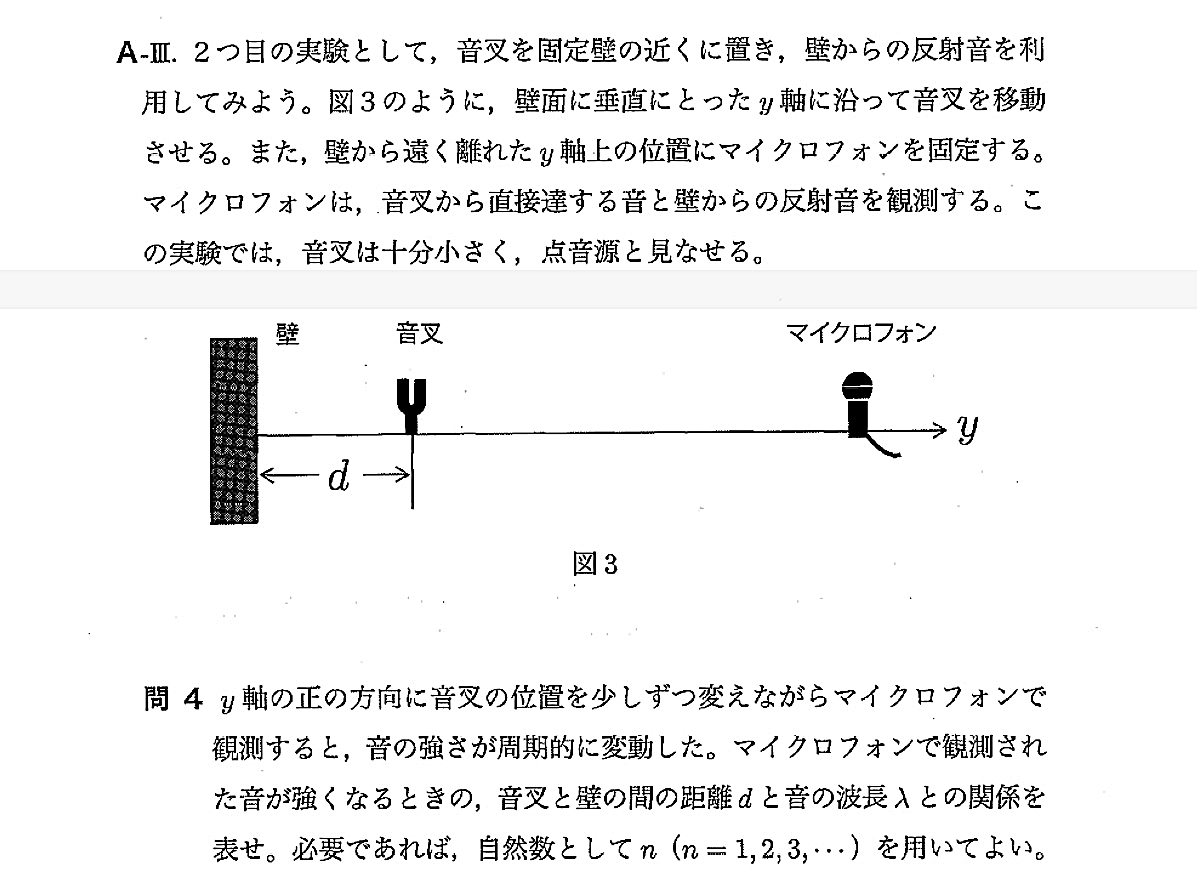
これだけ読むと随分難しそうなのですが、オーディオをやっている人間にとっては勘所はピンとつかめるはずです。
スピーカーは音叉なんかよりははるかに複雑な波形を含んだ音を出していますし、さらには音叉とは違って連続的に音を出していますから、この問題とは比べものにならないくらい複雑な物理現象です。

ただし、経験則として、スピーカーと背面の壁との距離をどうとるかは、音質を追い込んでいく上ではきわめて重要なことは嫌と言うほど知っています。
ですから、音叉（スピーカー）からマイクロフォン（リスナー）に直接届く直接波と、壁に跳ね返って帰ってくる間接波の関係を問うていることはすぐに理解できるはずです。

言うまでもないことですが、この直接波と間接波がピッタリ重なったときに音は最も大きくなり、逆にそれが反転した状態になるときに最も小さくなります。
そんな事はオーディオをそれなりにやっている人間にとっては常識に属する問題であって、「こんな専門的で難解な問題を解くために日夜頑張っている受験生が可哀想」などというのは大間違いなのです。

つまりは、その直接波と間接波がピッタリ重なる位置を、波長の「λ」と壁からの距離「d」で、そしてその重なる位置は繰り返しあらわれるので、その繰り返し現れる状態に関しては自然数「n」を使って表せと言うのです。
大学受験などというのはもう40年以上も前の話であり、基本的に文系頭なのでもしかしたら勘違いがあるかもしれませんが、まあ、オーディオ的に考えればそれほど外してはいないと思います。
あまり偉そうなことは言えませんが、物理の問題としては基本に属するような問題ではないでしょうか。

それでは、どうしてこういう基本的な問題でミスが発生したのでしょうか。
それは、どうやら高校の教科書では、反射する壁の状態を現実にはあり得ない理想的な状態として教えているらしいのです。
その理想的な状態とは、波を反射する壁が一切振動しないと仮定するのです。

これを、「固定端反射」というそうです。
こういう理想的な状態で波が壁にぶつかると、波形が反転します。

分かりやすい説明がYoutybeにありました。

この状態を仮定すると、どうやら（＾＾；波長の長さの1/4（半波長のさらに半分）だけずらせた位置に音叉をおけば直接波と間接波は重なって最大になるようで、あたえられた数字を使って一般式とすれば、阪大が正解とした「2d=(n-1/2)λ」となるようです。
つまりは、オーケストラのピッチの基本となる「A音」を例に考えると波長はザックリと80㎝ですから、その数値を代入すると、壁から20㎝、60㎝、100㎝・・・のところで最大になるというわけです。

しかし、現実問題として、波がぶつかった壁はその力によって振動するのが一般的であり、阪大の問題作成者が想定したような「固定端反射」等というようなものは物理的にはほぼ存在しないのです。
そして、波がぶつかったときに壁も振動するというごく当たり前の状態の事を「自由端反射」というそうです。

困るのは、この「自由端反射」では跳ね返った波は反転しないで、そのまま折り返して帰ってくる事です。
そのまま反転しないで折り返して間接波が帰ってくれば、音叉は波長の半分の位置に置けば直接波とピッタリ重なることになります。

文系頭ではなかなか正確に表現できないのですが、この違いは真逆であることは事実です。
そして、解答も「固定端反射」は半波長の奇数倍だったものが、「自由端反射」では半波長の偶数倍になっています。

それを一般式で表せば、「2d=nλ」となって、今回あらたに「正解」となったものです。
「A音」を例に考えると、ザックリと壁から40㎝、80㎝、120㎝・・・のところで最大になるというわけです。

なお、阪大がもう一つ「2d=(n-1)λ」も正解したのは、音叉を壁にくっつけた状態も良しとしたためで、そうすると、0㎝、40㎝、80㎝、120㎝・・・のところで「A音」ならば最大になるという事になります。

なお、この数字を眺めていて気づいたのは、オーディオにおける低域の処理の難しさです。
波長は伝播速度を周波数で割れば計算できますから、例えば80Hzあたりの音だと波長は4メートルを超えます。
背面の壁は当然の事ながら「自由端反射」ですから、半波長の偶数倍ごとに、つまりは2メートルごとにピークがくることになります。そして、2メートル以下ではとぐろを巻いてしまうことは容易に察せられます。

となれば、2メートルから4メートルの間で最適ポイントを探すのが理想と言うことになるのですが、そんな事はほとんど現実問題として不可能です。
ちなみに、40Hzならば4メートル、20Hzならば8メートルが必要と言うことになります。

ということは、オーディオにおける低域というのは理想的な形では処理できないという割り切りのもとに、自らの感性をフルに活用して無理と無理を重ね合わせることで納得のいく形に追い込んでいくしかないと言うことのようです。

なお、最後に余談ながら、今回の件について阪大の問題作成者のことを若者の青春を奪った極悪人のように言う向きもあるようですが、それは少し違うだろうという気はします。
おそらく、今回のミスの根っこには高校の教科書では波の反射は「固定端反射」として扱っていることがあるようで、そうなるとその責任の少なくない部分は学習指導要領を作成している文科省にあるということは見ておく必要があります。

ですから、今回の一番の問題は問題作成にミスがあった事ではなくて、ミスの指摘があったときに真摯に対応しなかったことでしょう。
とは言え、起こってしまったことはもとに戻るわけもなく、あらためて合格となった人たちは前向きに一歩を踏み出してほしいと思います。